The Computer Myth - Boolean Arithmetic (Part 03)
컴퓨터가 수행하는 모든 수학적, 논리적 연산은 ALU(Arithmetic Logic Unit)라는 칩이 담당한다. 우리가 지난번까지 본 NAND, AND 게이트들은 논리 연산을 수행하는 애들이다. 이들은 하나 이상의 boolean 값을 입력받아 특정한 논리 연산을 수행하고 하나 이상의 boolean 값을 내뱉는다. 하지만 ALU는 덧셈, 뺄셈과 같은 수학적 연산도 수행해야 한다.
수학적 연산을 하려면 우선 숫자라는 개념을 표현할 수 있어야 한다. 컴퓨터는 이진법으로 숫자를 표현한다. 즉 4(10)는 100(2), 8(10)은 1000(2), 9(10)는 1001(2) 식으로 나타낸다. 근데, 여기엔 문제점이 하나 있다. 만약 이처럼 각각의 숫자가 서로 다른 길이의 bit로 표시되면 모호성이 생긴다. 예컨대, 1100이라는 bit 나열이 있으면, 1100을 하나로 묶어서 12(10)라고 읽어야할까? 아니면 1와 100을 따로 보고 1(10)과 4(10)로 읽어야 할까?
그래서 컴퓨터는 모든 명령어의 길이를 고정시킨다. 흔히 32bit, 64bit 프로세서라고 부르는 것이 이 개념이다. 32bit 프로세서는 32bit를 하나의 단위로, 64bit 프로세서는 64bit를 하나의 단위로 본다. 그래서 만약 32bit 체계에서 4(10)를 표현한다면 0000 0000 0000 0000 0000 0000 0000 0100이 되고(띄어쓰기는 단순히 읽기 편하기 위해), 8(10)이라는 값은 0000 0000 0000 0000 0000 0000 0000 1000이 된다. 길이가 고정이므로 모호성이 사라진다.
우리가 설계할 컴퓨터는 16bit 컴퓨터다. 즉, 모든 명령어는 16bit로 이루어진다. 그래서 4(10)는 0000 0000 0000 0100이 되고, 8(10)은 0000 0000 0000 1000이 된다. 우리가 앞으로 보게 될 다양한 명령어들도 모두 16bit로 이루어질 것이다.
잠깐 딴길로 샜는데, 아무튼 ALU 칩을 만들기 위해서는 논리적 연산 뿐만 아니라 수학적 연산도 수행할 수 있어야 한다. 그래서 우선, 컴퓨터에서 숫자 개념을 표현하기 위해 이진법을 사용한다는 것을 알았다. 곧 이들끼리의 덧셈, 뺄셈과 같은 연산도 구현할 것이다. 이처럼 boolean값들로 숫자 체계를 표현하고, 이들끼리의 수학적 연산을 정의하는 것을 boolean arithmetic이라 부른다.
우리가 컴퓨터에서 표현할 수 있는 숫자의 범위는 제한되어 있다. 명령어의 길이에 따라 다르다. 예컨대, 4bit 컴퓨터가 있다고 한다면, 0000 ~ 1111 까지의 범위밖에 표현하지 못하므로 표현할 수 있는 숫자의 갯수는 24개, 즉 16개이다. 8bit 컴퓨터에서는 28개, 즉 256개가 되겠고, 16bit 컴퓨터에서는 216개, 즉 65536개가 된다.
따라서, 4bit 컴퓨터를 예로 들면, 0(10)은 0000이고 15(10)는 1111이 될 것 같다. 하지만 아니다. 이러면 음수값을 표현할 수 없게 된다. “음? -15는 -1111 이라고 쓰면 되는거 아닌가?” 헷갈릴만 하지만, 컴퓨터는 -라는 부호를 이해하지 못한다. 컴퓨터는 0과 1만 이해한다. 따라서, -1111이라는 음수 개념을 표현할 수 있는 다른 방법이 필요한데, 이를 위해 2’s complement라는 기법을 사용한다.
2’s complement는 이진법 체계에서 음수를 표현하기 위한 한가지 방법이다. x라는 양수가 있을 때, 이의 음수값은 2n - x 로 정의한다. 즉, x + (-x)는 항상 2n이 되기 때문에 2’s complement라고 불린다.
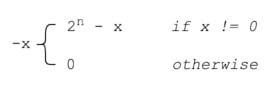
예를 들어, 4bit 체계에서 -3을 표현하자면 24 - 3 = 13, 즉 1101이 된다. 마찬가지로 -1은 24 - 1 = 15, 즉 1111이 된다. 4bit 체계에서 표현할 수 있는 모든 수는 아래와 같다:
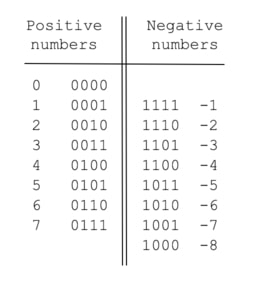
이 기법을 사용한 결과로, 양수는 가장 왼쪽의 bit(Most Significant Bit)가 0이고 음수는 1이라는 특징이 생긴다. 그리고 표현 가능한 숫자의 범위는 -2n-1 ~ 2n-1 - 1이 된다. 참고로, nbit 체계에서 x라는 숫자의 부호를 바꾸려면 2n - x를 하면 된다고 했는데, 쉽게 계산할 수 있는 공식으로 모든 bit를 반전(NOT) 후 1을 더하면 된다. 예컨대 -3(10)은 3(10)을 나타내는 0011을 반전시켜 1100로 만든 후 1을 더해 1101이라고 구할 수 있다.
정리하자면, 컴퓨터는 모든 숫자를 이진법으로 나타낸다. 그리고 모호성을 없애기 위해 하나의 숫자(또는 명령어)를 표현하는 bit의 길이를 고정시킨다. 예컨대, 16bit 시스템에서는 항상 16개의 bit를 한 단위로 보고, 32bit 시스템에서는 32개의 bit를 한 단위로 본다. 또한, 양수와 음수를 표현하기 위해 2’s complement라는 기법을 이용한다. 그래서, 보통은 nbit 체계에서 0 ~ 2n - 1 사이의 값을 나타낼 수 있겠지만, 이 기법을 도입하여 -2n-1 ~ 2n-1 - 1 사이의 값을 나타낼 수 있게 된다. 모든 양수는 가장 왼쪽의 bit(MSB)가 0이 되고 음수는 1이 된다는 특징을 지니게 된다.
컴퓨터에서 숫자를 표현할 수 있게 되었다! 이진법, 십진법의 개념에 익숙치 않은 분들은 머리가 아주 복잡복잡할 것이다. 잘 이해가 되길 바라며.. 다시 찬찬히 읽어보기를 추천한다. 다음 포스트에서 볼 ALU 칩은 지금까지 우리가 쌓아온 논리 연산 게이트들과 숫자 체계를 기반으로 만들어질 것이다. 앞서 말했듯이, 우리는 16bit 컴퓨터를 만든다. 즉, 모든 데이터(숫자)와 명령어는 항상 16bit로 표현된다. 따라서, 이전에 본 1bit 단위로 동작하는 NAND, AND 등의 게이트들을 16bit 단위로 동작하도록 확장시키고, 이들을 재료로 삼아 16bit 단위로 모든 연산을 수행하는 ALU 칩을 완성시켜 나갈 것이다.

Leave a comment